パラドックスの不思議

「パラドックス（paradox）」とは、正しそうに見える前提と、妥当に見える推論から受け入れがたい結論が得られる事を指す語である。

パラドックスは

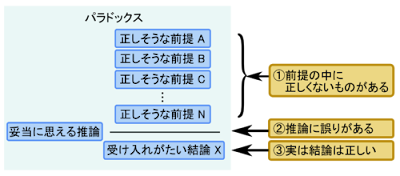
• 論理的に矛盾しているもの
• 直感的には受け入れがたいが矛盾はしていないもの

に分けられる。前者を一般的にパラドックスと呼ばれ、広く区切ると後者もそれに入る。

パラドックスという言葉は数学界で主に用いられ、それ以外の分野では、「ジレンマ」、「矛盾」、「意図に反した結果」、「理論と現実のギャップ」等の言葉が用いられる。

以下では、パラドックスの具体的な例を挙げていく。

自己言及のパラドックス（The paradoxes of self-reference）

クレタ人が「クレタ人はすべて嘘つき」と言った。

「この文は偽である」が真なら、それは偽だということになり、偽ならばその内容は真ということになり……というように無限に連鎖する。

同様に「この文は偽である」が偽なら、それは真ということになり、真ならば内容から偽ということになり……と、この場合も無限に連鎖する。

ラッセルのパラドックス（Russell's paradox）

「ある村でたった一人の男性の床屋は、自分で髭を剃らない人全員の髭を剃り、それ以外の人の髭は剃らない。この場合、床屋自身の髭は誰が剃るのだろうか？」

• 床屋が自分の髭を剃らなければ、彼は規則に従って、髭を自分で剃らなくてはいけなくなり、矛盾が生じる。
• 床屋が自分の髭を剃るならば、「自分で髭を剃らない人の髭を剃る」という規則に矛盾する。

したがって、この規則はどちらにしても矛盾してしまうことになる。

ゼノンのパラドックス（Zeno's paradox）

「飛んでいる矢は止まっている」

これは物体の運動に関するものである。矢が飛んでいる様子を考えよう。

ある瞬間には、矢はある場所に位置している。僅かな時間だけに区切って見れば、矢はやはり少ししか移動しない。この時間をどんどん短くすれば、矢は動くだけの時間がないから、その瞬間だけは同じ場所に留まっているであろう。

次の瞬間にも、同じ理由でやはりまた同じ場所に留まっているはずである。こうして矢は、どの瞬間にも同じ場所から動くことはできず、ずっと同じ場所に留まらなくてはならない。したがって飛んでいる矢は止まっている。

砂山のパラドックス（Paradox of the sandpile）

砂山から砂粒を個々に除去していくことを想定する。ここで、次のような前提から論証を構築する。

1.     「砂山は膨大な数の砂粒からできている」（前提1）

2.   　「砂山から一粒の砂を取り除いても、それは依然として砂山のままである」（前提2）

前提2 を繰り返し適用したとき（つまり、毎回砂山の砂粒数は徐々に減っていく）、最終的に砂山の砂粒が一粒だけになる。

前提2 が真であるなら、この状態も「砂山」だが、前提1 が真だとすれば、このような状態は「砂山」ではない。これが矛盾である。

バター猫のパラドックス（Buttered Cat Paradox）

これは2つの言い伝えを皮肉った組み合わせに基づいた逆説である。

• 猫は常に足を下にして着地する
• バターを塗ったトーストは常にバターを塗った面を下にして着地する（選択的重力の法則）

もしバターを塗ったトーストを（バターを塗った面を上にして）猫の背中へくくり付けて、ある高さから猫を落としたらどうなるかを考えた場合、この逆説が発生する。

動物愛護団体から来るであろう抗議にもかかわらず、もし実際に猫を落とすならば、2つの最終結果のうちのどちらか一方は決して起こらないことになる。

もし猫が足を下にして着地すれば、トーストはバターが塗られた面が上になったままだし、

逆にバターが塗られた面が下になって着地するならば、猫は背中から着地することになるはずだ。

抜き打ちテストのパラドックス（Paradox of the test spot）

ある教師が、学生たちの前で次のように予告した。

来週の月曜日から金曜日までのいずれかの日にテストを行う。抜き打ちテストであり、テストが行われる日がいつかはわからない。

• 　まず、金曜日に抜き打ちテストがあると仮定する。すると、月曜日から木曜日まで抜き打ちテストがないことになるから、木曜日の夜の時点で、翌日（金曜日）が抜き打ちテストの日であると予測できてしまう。これは抜き打ちとは言えないので、金曜日には抜き打ちテストを行うことができないということが分かる。

• 　次に、木曜日に抜き打ちテストがあると仮定する。すると、月曜日から水曜日まで抜き打ちテストがないことになるから、水曜日の夜の時点で木曜日か金曜日のどちらかの日に抜き打ちテストがあることが予測できるが、1. により金曜日には抜き打ちテストがないことが既に分かっているので、翌日（木曜日）が抜き打ちテストの日であると予測できてしまう。よって、木曜日にも抜き打ちテストを行うことができないということが分かる。

• 　以下同様に推論していくと、水曜日、火曜日、月曜日にも抜き打ちテストを行うことができないということが分かる。したがって、「先生はいずれの日にも抜き打ちテストを行うことができない」という結論になる。 

しかし翌週、テストは水曜日に行われた。上記の推論にもかかわらず、学生は全くテストの日を予測できなかった。

すべては教師の予告通りになった。

テセウスのパラドックス（Theseus' paradox）

テセウスの船の全部の部品が置き換えられたとき、その船が同じものと言えるのか。

他にも

• 置き換えられた古い部品を集めて何とか別の船を組み立てた場合、どちらがテセウスの船なのか。
• テセウスの船を解体して、その部品を全て使って“家”を作った。そしてそれをまた解体して再び船を作った。これはテセウスの船と呼べるか？ 

という疑問が生じる。

パラドックスは奥が深い。
果たして、真相が出るときは来るのだろうか。